 For the past thirty years I’ve been corresponding with my high school calculus teacher, Mr. Don Joffray. During that time, he went from the prime of his career to retirement, competed in whitewater kayak at the international level, and lost a son. I matured from teenage math geek to Ivy League professor, suffered the sudden death of a parent, and blundered into a marriage destined to fail.
For the past thirty years I’ve been corresponding with my high school calculus teacher, Mr. Don Joffray. During that time, he went from the prime of his career to retirement, competed in whitewater kayak at the international level, and lost a son. I matured from teenage math geek to Ivy League professor, suffered the sudden death of a parent, and blundered into a marriage destined to fail.
In an excerpt from his new memoir, a Cornell math professor ponders the life lessons garnered from decades of correspondence with his high school calculus teacherWhat’s remarkable is not that any of this took place—such ups and downs are to be expected in three decades of life—but rather that so little of it is discussed in the letters. Instead, our correspondence, and our friendship itself, is based almost entirely on a shared love of calculus.
It never occurred to me how peculiar this is until Carole (I’m happily remarried now) teased me about it. ”You’ve been writing to him for thirty years? You must know everything about each other.” Not really, I said. We just write about math problems. ”That is such a guy thing,” she said, shaking her head.
Her question got me thinking. What did I really know about my teacher? Why had so much gone undiscussed between us? On the other hand, we both enjoyed our correspondence the way it was, so was there any problem here?
Questions like these have kept nagging at me. I’m not sure how to go about answering them or if I should even try. All the while, I find myself looking for clues in a green Pendaflex folder in my office, stuffed four inches thick with letters about math problems.
I WAS FIFTEEN WHEN I TOOK CALCULUS FROM MR. Joffray. One thing about him was unlike any other teacher I’d ever had: he worshipped some of his former students. He’d tell stories about them, legends that made them sound like Olympian figures, gods of mathematics. In my own case, he was more a fan than a teacher, always marveling at what problems I could invent and solve. It felt slightly strange to be so admired by my own teacher. But I can’t say I minded it.
After I graduated, something in me wanted to stay in touch with him. My first letters were about math problems that I thought he’d enjoy, gems I’d picked up in my college courses. The letters were infrequent, about one a year. I suppose he must have written back to me, but none of his responses have survived. It never occurred to me to save them.
It was only a decade later, when I was just starting my career as a professor, that our correspondence began to flourish. The pattern was always the same: Mr. Joffray would write to ask for help with a problem that had stumped him, typically a question raised by one of his seniors in the most advanced math class at the school. When one of these letters arrived in the mail, I stopped whatever I was doing to see if I could help. For one thing, they posed fascinating little questions, beautiful excursions off the beaten track of calculus. But maybe more important, they gave me a chance to explain math to someone who loved learning it, the best student any teacher could have—someone with perfect preparation and an evident sense of delight and gratitude.
With his retirement a few years ago and no more students to stimulate him, our correspondence began to wane. Not in frequency—in fact, he wrote to me more than ever—but in intensity and reciprocity. It got to the point where I simply couldn’t keep up with him. Yes, he reassured me, he understood all that, and urged me not to worry; he knew how busy I must be in my career and with all the new obligations that come with raising a family. But it still felt like we were drifting apart. Ironically, I was now the same age that he was when he taught me in high school.
In January 2004, yet another letter arrived. But this time I felt anxious when I saw the envelope. The uncharacteristically tremulous handwriting reminded me of my dad’s after his Parkinson’s had set in.

Sat. January 17, 2004
Dear Steve, Eek! I had a mild stroke Thurs. noon and lost all sensation in my right (writing) hand. Several hours later I managed to open and close my fingers and get some strength back into my grip, but, alas, no dexterity! X@#! A one-handed piano player isn’t in demand, so I’ll miss my gig with our jazz quartet tomorrow. . . .
This glimpse of mortality awakened me to how much I’d been overlooking all these years. I felt compelled to visit Mr. Joffray at his home, to come to know the man behind the math.
Like calculus itself, this story is an exploration of change. It’s about the transformation that takes place in a student’s heart.CALCULUS IS THE MATHEMATICAL STUDY OF CHANGE. ITS ESSENCE IS best captured by its original name, ”fluxions,” coined by its inventor, Isaac Newton. The name calls to mind systems that are ever in motion, always unfolding.
 Like calculus itself, this story is an exploration of change. It’s about the transformation that takes place in a student’s heart, as he and his teacher reverse roles, as they age, as they are buffeted by life itself. Through all these changes, they are bound together by a love of calculus. For them it is more than a science. It is a game they love playing together—so often the basis of friendship between men—a constant, while all around them is in flux.
Like calculus itself, this story is an exploration of change. It’s about the transformation that takes place in a student’s heart, as he and his teacher reverse roles, as they age, as they are buffeted by life itself. Through all these changes, they are bound together by a love of calculus. For them it is more than a science. It is a game they love playing together—so often the basis of friendship between men—a constant, while all around them is in flux.
HAVING FINISHED THE MATH COURSES OFFERED BY THE SCHOOL, I spent my senior year teaching myself, detached from Mr. Joffray. I’d sit alone for an hour every day in an empty classroom, reading a textbook on multivariable calculus or trying to rederive Huygens’s results about cycloidal pendulums.
At other times I did a kind of research, often about chase problems. These problems of pursuit, as mathematicians call them, completely captivated me.
 The first one I ever heard of came from Mr. Joffray. It went like this: Suppose a postman is trying to escape from a dog chasing him. The postman starts at the origin and runs away in a straight line at a constant speed v. Meanwhile, the dog starts at a point somewhere off that line and runs with constant speed w, instantaneously swerving in such a way that it is always heading straight toward the postman’s current location. Find the equation for the curve traced out by the dog. [Diagram 1]
The first one I ever heard of came from Mr. Joffray. It went like this: Suppose a postman is trying to escape from a dog chasing him. The postman starts at the origin and runs away in a straight line at a constant speed v. Meanwhile, the dog starts at a point somewhere off that line and runs with constant speed w, instantaneously swerving in such a way that it is always heading straight toward the postman’s current location. Find the equation for the curve traced out by the dog. [Diagram 1]
Another one was quintessential Joffray: A man in a kayak, paddling across a river, is trying to reach a certain point on the opposite shore. The kayaker, being a determined and not-too-clever sort, always aims directly toward his destination even as he’s being carried downriver by the current.
Suppose that the river flows with constant speed v and the kayaker paddles with constant speed w relative to the river. Find the path traced out by the kayak. [Diagram 2]
These two chase problems—the dog and postman, and the determined kayaker—are both exercises in differential equations. Such equations are what calculus is all about: flux and change. A differential equation describes how a system changes its behavior in response to the ever-changing forces on it. All the pushes and pulls nudge the system to be in some new condition, or some new place, where the forces are different again. For instance, in the dogvs.-postman problem, the man keeps moving, so the dog has to keep revising its directional heading. It does that instantly.
That’s the breathtaking idea behind all of calculus—you think about what’s happening at an instant, in an infinitesimal unit of time—and you can actually deal with that ineffable idea, make it into a powerful predictive tool. Here we can write down a differential equation that captures the idea of ”aiming,” of the fact that the dog changes its course heading at every instant. And by solving that equation, we learn the whole path that the dog must follow. The whole trajectory is built of all the infinitesimal steps the dog takes en route to its prey.
This vision of the world—that everything can be viewed as the accumulation of infinitesimal changes—is the most revolutionary insight of calculus. Figuring out how to turn this idea into workable mathematics was the breakthrough that allowed calculus to be invented in the first place, back in the 1600s. Isaac Newton was trying to calculate how the planets move. He did this by thinking of the planets as being acted on by the ever-changing force of gravity. As they orbit the sun, they change their distance from it, which changes the gravitational tug they feel, which then steers them to a new place in the next instant, where the force is again slightly different, and so on. Solving for the motion of the planets becomes a problem in differential equations.
So by playing with chase problems, you can feel like you’re in the company of Newton. And you are. I loved that about them.
THE CHASE PROBLEMS THAT MR. JOFFRAY HAD TOSSED OUT WERE challenging but ultimately manageable. Their compliant character reinforced my feelings about mathematical justice. All you had to do was translate the word problem into the right equations; find the right substitutions; work calmly and logically and grind though the algebra without doing anything wrong; and sure enough, the right answer would pop out. It had to.
The first hint that something was wrong with this gauzy vision came when I concocted a question of my own. It seemed a lot like the other chase problems I’d solved, but for some reason it was turning out to be strangely obstinate. I spent months on it. It was frustrating, tantalizing, and delicious. With enough effort, I felt sure I could solve it, and all the months of frustration would make the conquest that much sweeter.
 The question was, suppose a dog at the center of a circular pond sees a duck swimming around the circumference. The dog chases the duck by always swimming straight toward it. In other words, the dog’s velocity vector always lies along the line connecting it to the duck. Meanwhile, the duck takes evasive action by swimming around the edge of the pond as fast as it can, always moving counterclockwise. Assuming both animals swim at the same constant speed, find an equation for the dog’s path. [Diagram 3]
The question was, suppose a dog at the center of a circular pond sees a duck swimming around the circumference. The dog chases the duck by always swimming straight toward it. In other words, the dog’s velocity vector always lies along the line connecting it to the duck. Meanwhile, the duck takes evasive action by swimming around the edge of the pond as fast as it can, always moving counterclockwise. Assuming both animals swim at the same constant speed, find an equation for the dog’s path. [Diagram 3]
It’s clearly some sort of spiral that asymptotically approaches the circle where the duck is. But what’s the equation for such a spiral? Unlike the spiral of a tethered goat winding itself tighter and tighter around a tree, this is an expansive spiral, growing away from its center but limited by a circular boundary it can never cross. A fascinating path.
I couldn’t calculate it. I tried every conceivable change of variables and even managed to reduce the problem to a beautiful differential equation, one that looked like it should be tractable. But I could never solve that one either.
What I didn’t know yet was that some math problems are unsolvable. No explicit answer is possible; in this case, there’s no formula for the dog’s spiraling path. It’s indescribable in terms of the elementary mathematical functions we’re used to. You might say our language isn’t up to the task.
In later years I’d realize that this is the rule, not the exception. Most differential equations are unsolvable in the same sense. Our library of formulas isn’t rich enough to encompass them. Which makes those few problems we can solve—the ones they give you in high school—seem all the more precious.
THE THEORY OF RELATIVITY IS FOUNDED ON EMPATHY. NOT empathy in the ordinary emotional sense; empathy in a rigorous scientific sense. The crucial idea is to imagine how things would appear to someone who’s moving in a different way than you are.
At a time when it seemed absurd to claim that the earth moves around the sun, Galileo asked doubters to imagine being confined below deck in an enormous ship. There are no port-holes in your cabin, no way to see the coastline passing by. If the sea is calm and the boat is gliding straight ahead at a steady speed, how could you tell you are moving? You couldn’t. Any observation you’d make would be the same as if you were motionless. Pour wine into your glass, and it falls straight down, just as it would on dry land. That’s because everything in your cabin—the furniture, the air, the wine—would be moving right along with the ship. By the same reasoning, said Galileo, the earth could be moving and we wouldn’t sense it.
Three hundred years later, Einstein wondered what he would see if he were riding alongside a beam of light. Would the electromagnetic waves stand still, in violation of Maxwell’s equations? Would a distant clock seem to stop ticking? From questions like these came the special theory of relativity, with its shattering insights about time and space, mass and energy. Later he asked how the laws of physics would appear to an observer inside a plummeting elevator (assuming he retained his composure long enough to make observations).
As a teenager I revered Einstein. For his genius, of course, but also because he radiated kindness. Silly as it sounds, he was a big part of why I wanted to attend Princeton. I wanted to be near him, to walk in his footsteps. Soon after arriving, I dragged a few other freshmen along with me to gaze at his house.
Lately, though, I’ve started to see him differently. He wasn’t perfect. There was even something slightly sad about him. Though a playful man in many ways, he was aware of missing out on the deepest forms of human intimacy. ”I am truly a ‘lone traveler’ and have never belonged to my country, my home, my friends, or even my immediate family, with my whole heart,” he once wrote. For all his empathy in the abstract, Einstein remained curiously detached from the people closest to him.
 IN THE JUNE 1961 MATHEMATICAL GAMES COLUMN IN Scientific American, Martin Gardner posed a riddle that has become a favorite in courses on the psychology of creativity:
IN THE JUNE 1961 MATHEMATICAL GAMES COLUMN IN Scientific American, Martin Gardner posed a riddle that has become a favorite in courses on the psychology of creativity:
One morning, exactly at sunrise, a Buddhist monk began to climb a tall mountain. The narrow path, no more than a foot or two wide, spiraled around the mountain to a glittering temple at the summit.
The monk ascended the path at varying rates of speed, stopping many times along the way to rest and to eat the dried fruit he carried with him. He reached the temple shortly before sunset. After several days of fasting and meditation he began his journey back along the same path, starting at sunrise and again walking at variable speeds with many pauses along the way. His average speed descending was, of course, greater than his average climbing speed.
Prove that there is a spot along the path that the monk will occupy on both trips at precisely the same time of day.
You might want to think about this for a minute. Can you come up with a convincing argument why this has to be true? You don’t have to figure out where the magic spot is—its location will depend on the unknown details of how fast the monk walked, how long he paused, and so on. You just have to prove that such a spot must exist, somewhere.
Many people feel that this problem is impossible, that not enough information has been given. And it’s certainly true that you can’t solve it with words or algebra. Give it a try and then read on.
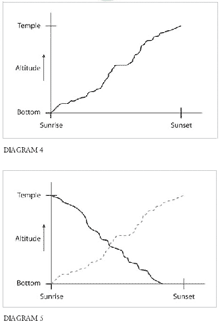 One approach is pictorial. Suppose we draw a graph of where the monk is at different times of day. On the ascent, the graph starts at the bottom at sunrise, then rises on a wiggly path (wiggly because of the monk’s pauses and variable walking speed), and finally reaches the top just before sunset. [Diagram 4]
One approach is pictorial. Suppose we draw a graph of where the monk is at different times of day. On the ascent, the graph starts at the bottom at sunrise, then rises on a wiggly path (wiggly because of the monk’s pauses and variable walking speed), and finally reaches the top just before sunset. [Diagram 4]
Now think about what the corresponding graph looks like on the way down. It’s another wiggly curve. We know almost nothing about its shape, except that it starts at the top and ends at the bottom. Fortunately, that’s enough information to solve the problem. When you put the rising and falling graphs on the same axes, it’s clear they have to cross each other somewhere. At that intersection point, the monk is at the same place at the same time on both days. [Diagram 5]
If you don’t find this argument convincing enough, you can make it more rigorous with calculus. Assuming that both curves are continuous functions of time (meaning that the monk moves continuously along the path and does not jump from point to point or use a jet pack), the intermediate value theorem guarantees that the rising and falling curves have to cross somewhere.
All this is fine, but it’s still not the best argument. The best argument uses only common sense and some imagination. It’s a nice example of the role of visualization in a mathematical proof.
Imagine the monk as two people, one climbing the mountain, one descending, and both starting at dawn on the same day. In other words, superimpose the events of both days and watch what happens. His climbing self will encounter his descending self somewhere on the mountain. And when he does, he’ll be at the same place at the same time. QED.
When I look back on where Mr. Joffray and I were in the fall of 1989, I’m reminded of the monk and the mountain. Our correspondence was about to take off like never before, right at the point where our careers began to cross, his descending and mine on the rise. We were now at the same place at the same time, though taking separate journeys.
EXCERPTED AND CONDENSED FROM THE BOOK ENTITLED THE CALCULUS OF FRIENDSHIP BY STEVEN STROGATZ, AVAILABLE NOW FROM PRINCETON UNIVERSITY PRESS. COPYRIGHT © 2009 PRINCETON UNIVERSITY PRESS. REPRINTED BY PERMISSION.


